First Order Motion Model for Image Animation
https://arxiv.org/abs/2003.00196
The improvement of the previous work of these authors - MonkeyNet. It allows you to animate an object in the image even better by the movements of another object. The disadvantage of MonkeyNet is that it didn't work well with a large change of "pose". Here Affine transformations to the local neighborhood of each keypoint are added. And also a prediction of the area to be inpainted is added. About MonkeyNet (which can help to understand this article) I wrote here https://evgenykashin.github.io/2020/06/09/MonkeyNet.html
Task: having the original image of the object and the target, transform the original object into the target pose. The high-level architecture has not changed much also Keypoint Detector, Dense Motion prediction, and Generator. Everything trains end2end and only on the video set from one domain with no labels. The main changes in obtaining dense optical flow.
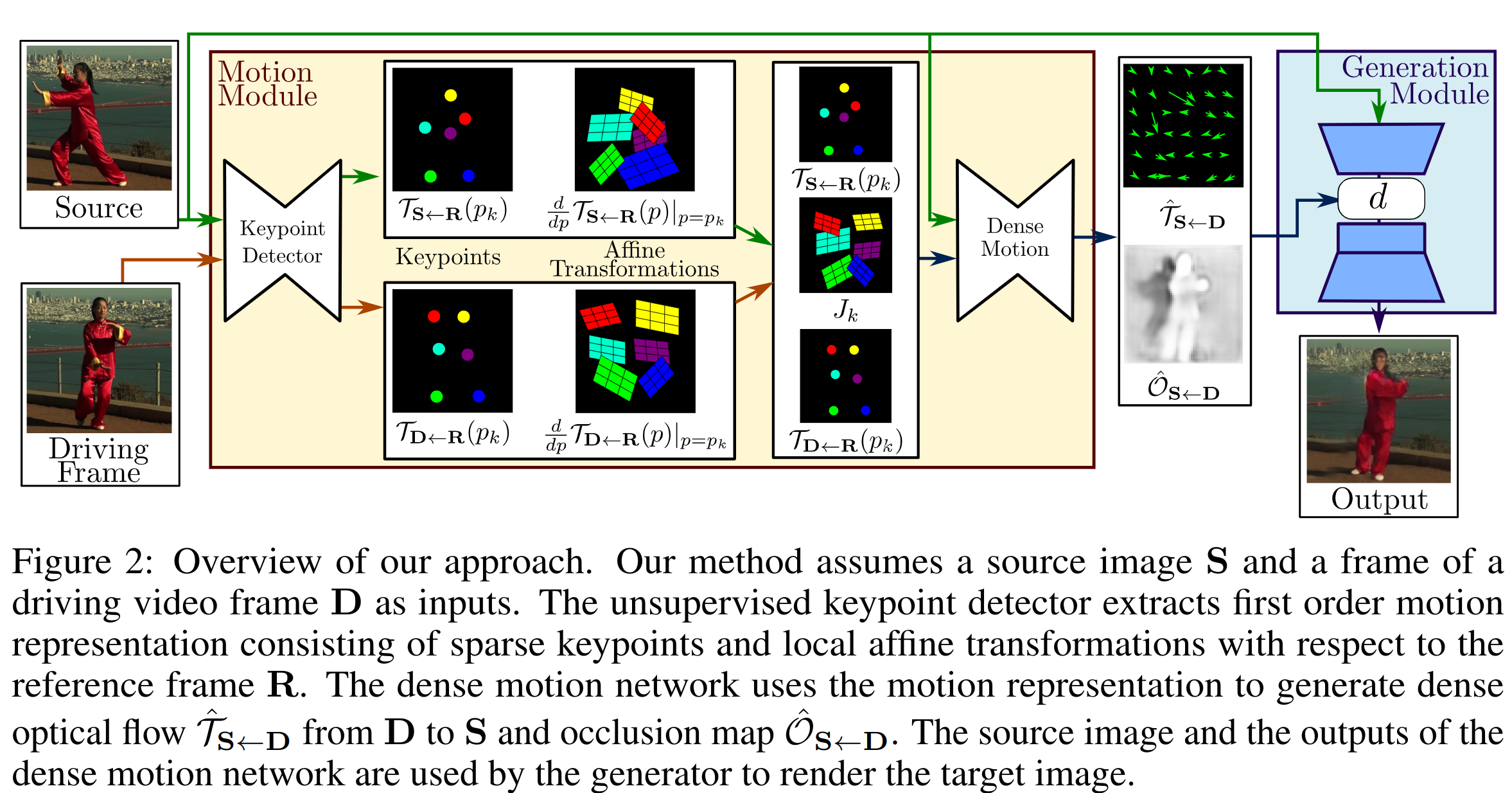
Keypoint Detector also self-supervised learns the position of keypoints, but now only keypoints centers are taken from the predicted UNet heatmaps, without covariance matrices. But now this block also predicts the Affine (linear) transformation matrix (2x2 - rotations and stretches, no shift) for each keypoints (locally).
The task of Dense Motion block remained the same - to predict dense optical flow by sparse keypoints(and now also by Jacobian matrices). To be more exact, the backward optical flow which for each pixel in target image D gives coordinates of the corresponding pixel in the original image S.

Backward optical flow, so it makes it possible to use differentiable F.grid_sample.
Back to Keypoint Detector. Besides keypoints for the source and target images, they now want to predict the Affine transformation for each keypoint. This makes it possible to simulate not only the shift of keypoints between source and target but also any rotations/stretches in the local neighborhood of the keypoint. They could probably predict one local transformation for each pair of source and target keypoints at a time, but they predict the transformation for the source and target keypoints separately. Sort of because the source and target images can be very different, and it better to predict independently for any image, without requesting the pair (as usually predicted in keypoints detection). But then it turns out for the source and target images 2 transformations are predicted, into some abstract frame R, which we will never see even. It's really abstract. After that two transformations will have to be merged into one S < - D.
How did they even come to local Affine transformations? It came from the idea of decomposing the backward optical flow into Taylor series in the neighborhood of a keypoint. When expanded in a series, we obtain a Jacobian matrix, since the initial function from 2d space to 2d space, the matrix has the size of 2x2, which in fact can be considered as a matrix of linear transformation (rotation, stretch, but without shift). In practice, a uniform 2d grid is obtained first (from -1 to 1 by x and y), shifted by the coordinates of the target's keypoint, then a linear transformation is applied to each point of the grid, and the resulting flow is obtained by shifting by negative coordinates of the source's keypoint. Thus, the first order due to the linear transform inside (2nd member of the Taylor series), if it is removed, we get zero order, which is essentially MonekyNet.
Backward optical flow from D to S can be obtained by combining the optical flow of the source and target keypoint into an abstract frame R.
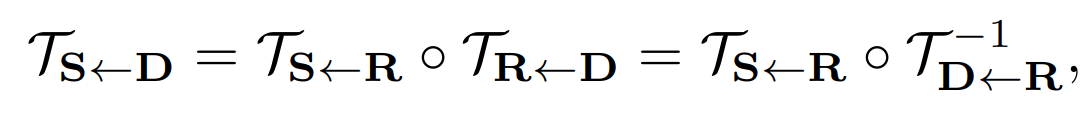
Decomposing this function in Taylor series (details in appendix):
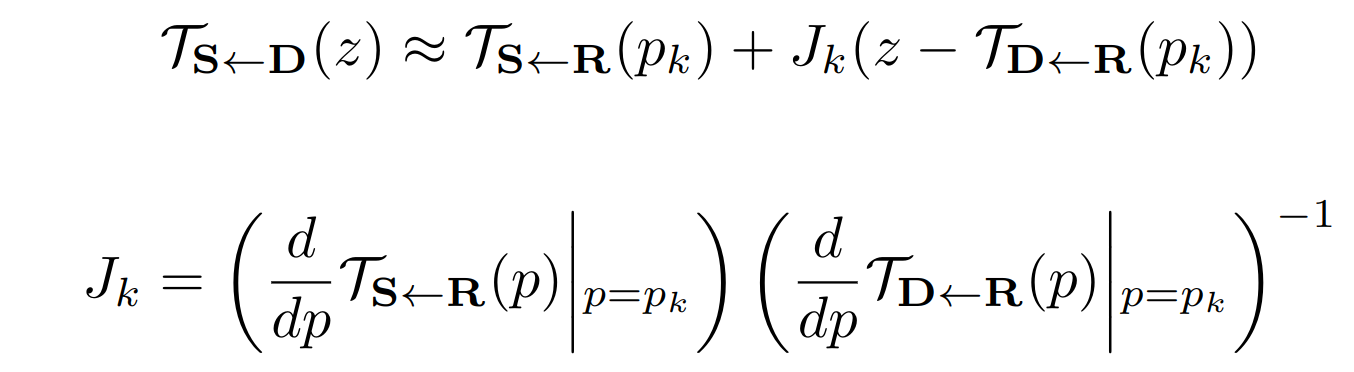
In the last formula, both multipliers (Jacobian matrices) are predicted by Keypoint Detector (4 numbers for each keypoint).
After getting the above sparse motion representation, it is possible to go to the Dense Motion block. Like MonkeyNet there is a UNet, which predicts for each keypoint the mask of the part of the object for which the keypoint is responsible (the local area of transformation), as well as an additional mask for the background. These masks can be used to aggregate local optical flows from all the keypoints into a single optical flow (by multiplying the masks by the corresponding flow and adding them all). The input to this UNet is the difference between the keypoints of two images (as in MonkeyNet - each keypoint has its own channel with a Gaussian difference, only now without covariance). Also, the input is given the original image, but as in the previous work, in a tricky way. To better match the area of a keypoint in the original image with that area in the target image, they make a copy of the original image for each keypoint and apply the corresponding keypoint transformation to it. Then everything is connected channel-wise. In this UNet and the one that predicts keypoints authors decided to optimize and work with 4 times smaller images.
The last Generation module should generate the original picture in a new pose. It takes the original picture to input, downsample it through several convolutional layers. With the optical flow obtained above, the activation tensor (after the downsampling) is warped. UNet from Keypoint Detector, in addition to the keypoints' masks, also generates an occlusion map [0, 1]. It should show from which area the warped activations can be taken and in which areas it is necessary to create (inpaint). Essentially, the warped activations simply multiplied by this occlusion map. The result goes into several ResNet blocks, and then into a convolution upsampling.

These are examples of occlusion maps. The dark part that can't be warped from the original features and has to be generated.
The main loss is the multiscale perceptual loss (pre-trained VGG19, but before that, it was a perceptual loss by the discriminator, it is not clear how much did it affect), also adversarial LSGAN loss. They also use Equivariance Constraint - a regularizer, which is usually used in works on unsupervised keypoint detection. It forces the prediction of keypoints in the same place before and after geometric augmentations (thinplate splines deformations) of the original image. This regularizer is applied to both predicted keypoints and the Jacobian matrices.
Like in MonkeyNet on the inference, they do not transfer the absolute movement, but the relative movement of the target object. During the train stage, there is no problem, because they train one person (different frames) on one video at a time. And at inference stage objects can be different sizes and in different parts of the image, so they transfer not the D_n position of the frame to S, but the difference of the position relative to the initial frame (roughly speaking) D_n - D_0. This means that the initial poses of the original object and the object that defines the movement must match. But it helps if the shape of the face/body of the source and moving person are not similar.
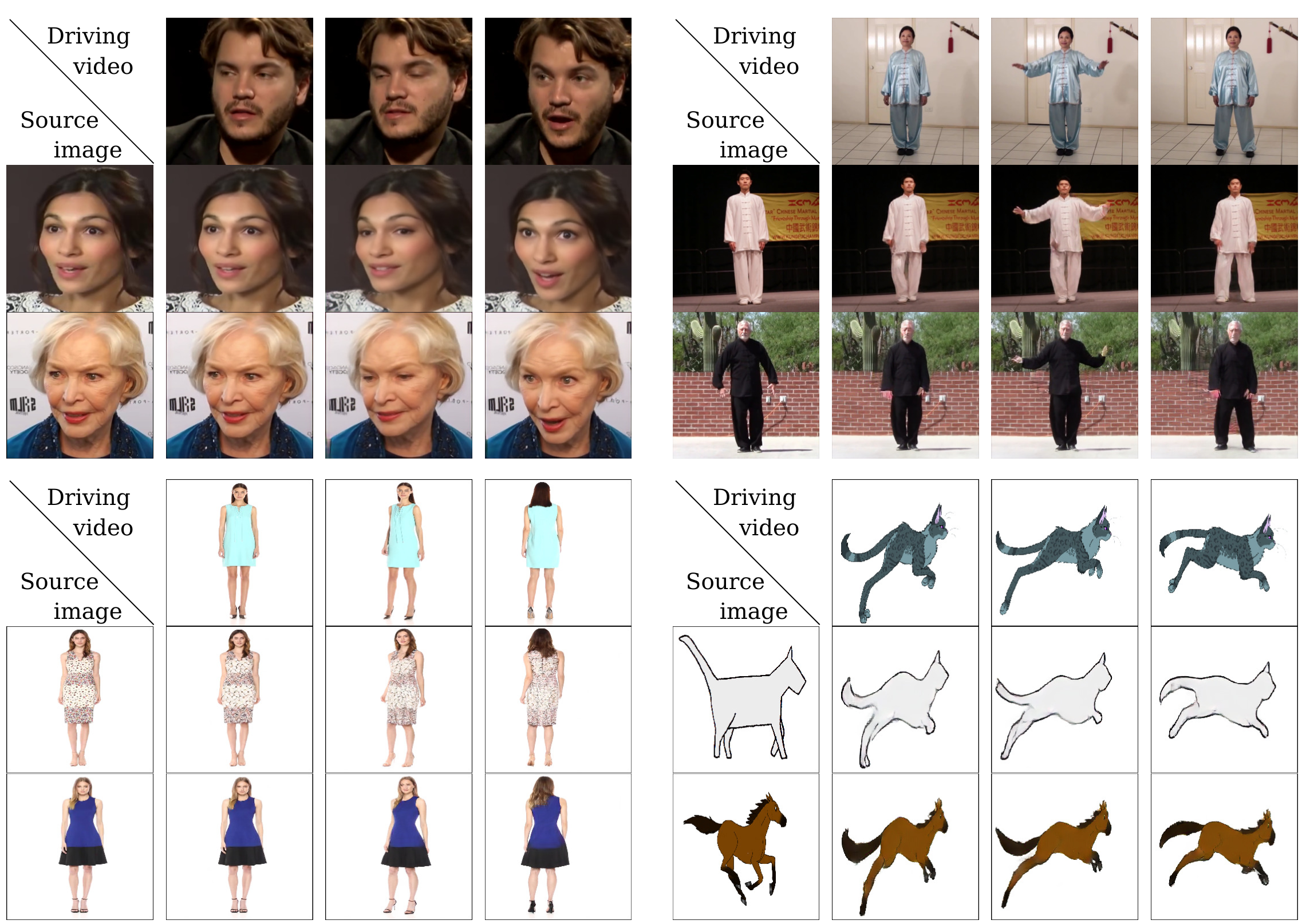
They tested on different datasets (faces, bodies, robots), beat up all competitors, especially when bending the bodies (local transformations are cool).

Good ablation study. For example, you can see that using local transformations without Equivariance Constraint is collapsing.

More results of the transformations.
